日前，数学科学学微分方程团队周立群教授及其合作者在自动化及人工智能领域的国际顶级学术期刊IEEE Transactions on Systems, Man, and Cybernetics- Systems（IEEE TSMC-S）（在JCR期刊AUTOMATION & CONTROL SYSTEMS类中排名为1/63，目前位列中科院期刊分区一区TOP）发表了题为“Global polynomial synchronization of proportional delayed inertial neural networks”的学术论文。

惯性神经网络（INNs）的同步性在保密通信中有着广泛的应用。由于网络运行过程中放大器的开关和信号传输导致时滞不可避免。比例时滞是一类无界时变时滞，可用于刻画惯性神经网络的时滞情况，但是比例时滞的无界性给神经网络的同步性研究带来了很大的挑战。该文提出了一种新的时滞微分不等式方法，研究比例时滞惯性神经网络的全局多项式同步性。

本文研究了以比例时滞惯性神经网络（PDINNS）作为驱动响应系统的全局多项式同步。通过设计易于硬件实现的反馈控制器，采用降阶法将所研究系统的误差系统降为一阶微分方程，应用拉格朗日中值定理、导数定义、构造辅助函数等方法以及矩阵和向量范数的性质，建立了范数形式的新型比例时滞微分不等式。通过应用新建立的比例时滞微分不等式，获得了所研究PDINNS的两个全局多项式同步的矩阵范数形式的判定准则，易于验证。该方法的创新性和优点是没有使用通常的构造Lyapunov泛函的研究方法，为惯性神经网络的动力学研究提供了新的研究方法及思路。  

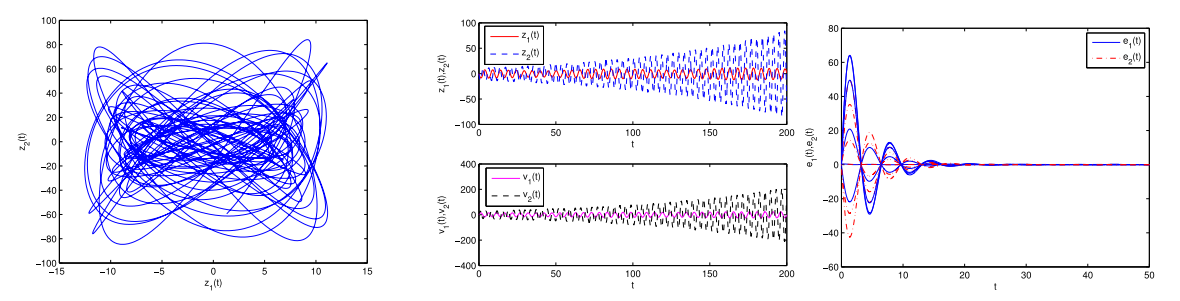
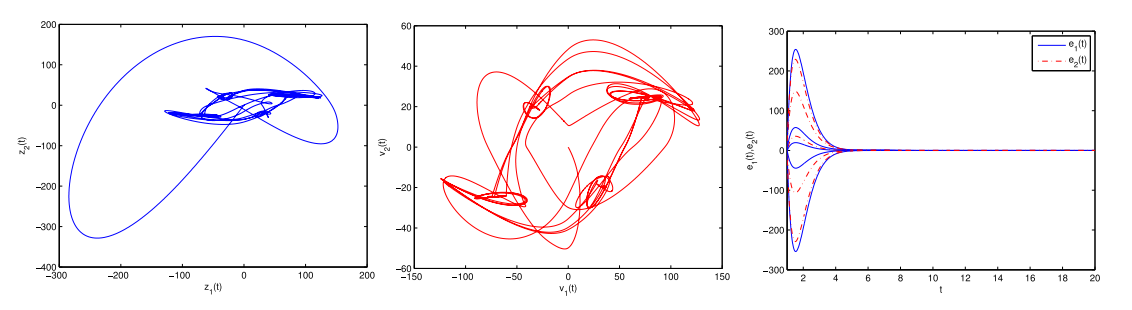
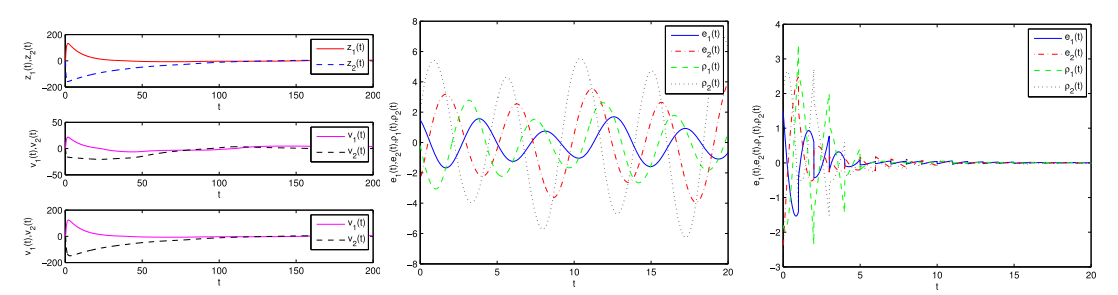
该项成果是必威微分方程团队周立群教授（第一作者）、湖南师范大学朱全新教授（通讯作者）与Texas A&M 大学黄廷文教授的合作共同完成。该研究获得国家自然科学基金面上项目(11901433、62173139)、天津市自然科学基金面上项目(18JCYBJC85800)和湖南省科技创新计划项目(2021RC4030)的资助。

必威微分方程团队近年来致力于比例时滞神经网络的动力学研究，在应用数学及交叉研究领域主流期刊IEEE TSMC-S、Inf Sci、Nonlinear Dyn、及ISA Trans等发表系列研究成果。

论文链接：https://ieeexplore.ieee.org/document/10068555